
Students in Grade 10 Math will learn many new and exciting concepts, one of which is Trigonometry. Trigonometry is a branch of mathematics that examines the relationship between the sides and angles of triangles. It’s beneficial to understand how Trigonometry works since it is applied in many fields, such as engineering and science. If you are in Grade 10 Math or are preparing to take Grade 10 Math, you’ve come to the right place. Here are some tips to help you succeed in Grade 10 Trigonometry.
Study the properties of a triangle.
- Before you dive into Trigonometry, you should have a solid understanding of the properties of a triangle.
- Triangles have three sides and three angles. There are different types of triangles, such as equilateral, isosceles, and scalene.
- Equilateral triangles have three equal sides and three equal angles. Therefore, equilateral triangles always have three 60° angles.
- Isosceles triangles have two equal sides, and scalene triangles have no equal side. This means that the angles will vary when looking at these triangles.
- Triangles can also vary by their angles.
- Acute triangles have angles that are less than 90°.
- Right angle triangles have one 90° angle.
- Obtuse triangles have one angle that is greater than 90°.
- Triangles can have the same angles, even if they are different in size. Check out this example:
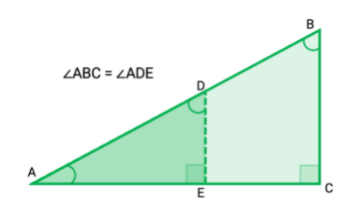
Get to know the Tangent Function.
- In Grade 10 Math, you will need to use Trigonometric functions to find the values of angles and sides of triangles.
- There are three Trigonometric functions that will help you solve these tricky math problems. First, we’re going to talk about the Tangent Function.
- The Tangent Function (“tan”) is used to find the slope angle or the hypothenuse length of a right-angle triangle.
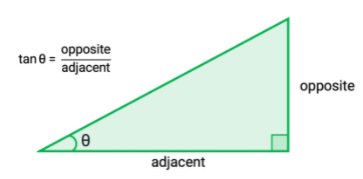
- Check out this sample problem below:
- We are looking for the angle θ. We are given the adjacent side of the triangle, which is 6cm, and the opposite side, which is 3cm.
- Using the tangent function, we can easily find the θ angle.
- First, rearrange the equation to isolate θ on one side of the equation. To do so, we must use the inverse tan function (tan-1).
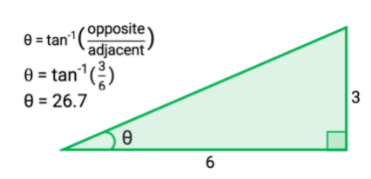
- To find the angle, you’ll need a scientific calculator. Look for the inverse tan function on your calculator and multiply it by 3/6.
tan-1(3 ÷ 6) = 26.7
- Therefore, the θ angle is 26.7°.
- You can also use the Tangent Function to find the length of the adjacent or opposite side of the triangle.
- Using the same triangle above, plug θ = 26.7 into the tan function and solve for the length of the opposite side. This will give you tan(26.7) = opposite/6.
- Rearrange the equation to isolate “opposite” onto one side of the equation.
- Use your calculator to multiply tan(26.7) × 6, and you will find it is equal to 3!
Learn about the Sine and Cosine Functions.
- Now you might be wondering about the other angles and sides.
- Sine and cosine are also Trigonometric functions you can use to find missing angles and sides of triangles.
- Before learning about the Sine and Cosine functions, it’s important to understand how to find the opposite side and the adjacent side of each triangle.
- The opposite and adjacent sides change if you’re looking at different angles. Check out the image below:
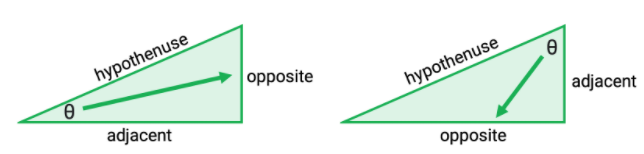
- Now that we’ve established the sides of the triangle, we can use Sine (“sin”) and Cosine (“cos”) to solve Trigonometry problems.
- The Sine Function is used for the opposite side and hypothenuse.
- The Cosine Function is used for the adjacent side and the hypothenuse.
- The best way to remember the Tangent, Sine and Cosine Functions is “SOHCAHTOA”.

- SOHCAHTOA stands for:
- Sine, Opposite, Hypothenuse
- Cosine, Adjacent, Hypothenuse
- Tangent, Opposite, Adjacent
- Now that you have the three Trigonometric Functions, you can solve all sides and angles of a triangle! The process is the same as the Tangent Function we saw above.
- If you are searching for an angle, you need to use the inverse function of Sine (sin-1), Cosine (cos-1) or Tangent (tan-1). If you are searching for the length of a side, use the regular function (sin, cos, or tan).
Review the concepts above, and practice, practice, practice!
- Just like every other math course you’ve taken in the past, you’ll need to work on practice problems as often as possible to succeed.
- Take time to review Trigonometry often and complete chapter reviews in your textbook.
- Always ask for help if you find a topic confusing. Filling your knowledge gaps will prevent small mistakes on quizzes and exams in the future.
If you follow the above tips, you’ll have everything you need to succeed in Grade 10 Trigonometry. Continue to work hard, and you can achieve anything you set your mind to. If you need help with Trigonometry, don’t hesitate to ask your teacher or a friend. Here at Success Tutorial School, we offer a number of programs designed to help students prepare for Grade 10 Math or assist those already enrolled. Contact us today to learn more about how we can help you or your child succeed in Grade 10 Math.


